
proposed a knot interval duplication and optimization method to obtain local knot vectors. , gap-free T-spline surfaces are generated by inserting zero-interval edges around the extraordinary points. In the template method proposed by Wang et al. Some methods have been developed to deal with the problems caused by extraordinary points. More details about the concept of extraordinary points are presented in section 2. When encountering an unstructured T-spline surface, the knot interval vectors about the vertexes around the extraordinary points are ambiguous. T-splines containing extraordinary points are called the unstructured T-splines. In complex T-spline models, the extraordinary points are always indispensable. So far, T-splines have been used in many fields such as geometric modeling, isogeometric analysis and shape optimization.
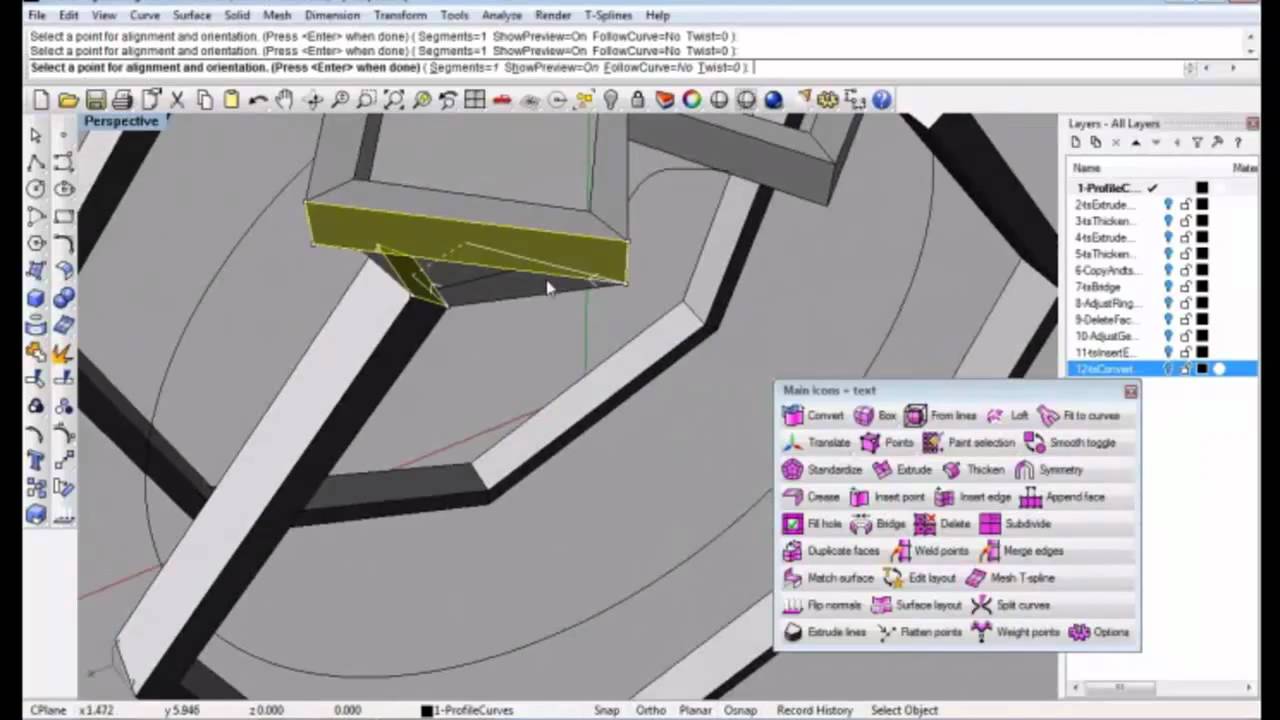
Analysis-suitable T-splines satisfy a simple topological requirement and their blending functions are linear independent. studied the linear independence of T-spline blending functions and proposed the notion of analysis-suitable T-splines. , multiple trimmed NURBS patches are merged into a single watertight T-spline surface. T-splines provide a promising way to breakdown these barriers. In addition, it is difficult to represent a complex model with a single NURBS surface and the gaps along the common boundary of two NURBS surfaces are unavoidable. This shortcoming can be overcome by T-splines which can achieve local refinement without introducing an entire row of control points. It requires a large number of superfluous control points to maintain the topological shape while implementing refinement. Firstly, a NURBS surface is defined in a rectangular topological grid. Compared with NURBS, the advantages of T-splines can be reflected in the following aspects.
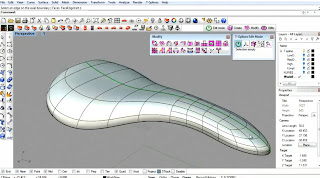
Theoretically, a T-spline surface can represent any arbitrarily shaped model no matter how complicated its topology structure is.
in 2003 to conquer the limitations of NURBS in practical engineering applications.Īs a generalization of NURBS, T-splines introduce T-junctions and extraordinary points into its control mesh. Thus, T-splines were firstly proposed by Sederberg et al. Nevertheless, in modern industry, complex engineering models comprised of multiple NURBS patches are always not watertight because of the existence of gaps and overlaps along the interfaces of trimmed NURBS surfaces.
#T spline rhino free download series#
With a series of excellent mathematical and algorithmic properties, non-uniform rational B-splines (NURBS) has been widely used in the field of computer aided geometric design for representing curves and surfaces.


 0 kommentar(er)
0 kommentar(er)
